The detail in an image is determined by resolution. That’s why calculating image resolution is a good knowledge to have. This note looks into how image resolution can be calculated.
The detail in an image is determined by resolution. That’s why calculating image resolution is a good knowledge to have. This note looks into how image resolution can be calculated.
There is not yet an industry standard for the level of sharpness required in every video surveillance application (detection or identification) or machine vision application (barcode or license plate reading). For security applications, the more pixels on a target, the higher the resolution will be, and the more likely recognition and positive identification will be made. It must be said, however, that higher detail requires higher resolution cameras or more cameras and thus more bandwidth and storage. There is a balance that must be made between level of detail and project budget.
Read More: How to differentiate between quality megapixel lenses
Read More: The tradeoff between field of view and resolution
Resolution can be expressed with the number of pixels of the image sensor. With megapixel cameras, resolution is generally expressed with the total number of pixels, divided by one million and rounded off.
Resolution can also be the level of detail with which an image can be reproduced or recorded. Commonly used by lens designers and optical engineers, image sensor resolution is expressed as line pairs per millimeter (lpm). As the total number of pixels on an image sensor increases, the pixel size gets smaller and requires a lens of higher quality to achieve focus.
Last, resolution can be specified in pixels per foot or meter at an object. It is basically the horizontal field of view (HFOV) of the camera divided by the horizontal number of pixels. This gives the number of pixels per foot that can be correlated to image quality. The rest of the article takes on this definition.
Wide angle field of view
An advantage of megapixel cameras is the ability to cover a much wider area with the same or better resolution compared to its analog counterparts. As available pixels across the field of view are greater, the field of view can be increased without decreasing image resolution.
Figure 1 compares the field of view of different cameras at a distance of 32 feet from the subject at the same image resolution. As the camera resolution (total number of pixels) increases, so does the field of view (pixels per foot). Clearly, the higher the number of pixels, the wider the field of view it acquires at a constant image resolution.
 Click to zoom in
Click to zoom in
The shorter the lens' focal length, the wider the field of view. With a view greater than 90 degrees, most wide-angle lenses will have barrel distortion (also known as fisheye distortion) where image look curved and bulged out in the center. Rectilinear lenses keep lines that appear straight in the real world straight on the image sensor. This increases the resolution at the edges; lenses with barrel distortion lead to compressed edges and reduced resolution.
With typical distorted wide-angle lenses, potentially valuable information is lost, and no software can reconstruct the lost information. Any dewarping will create an image that looks like that from a rectilinear lens but at lower resolution. With a rectilinear lens, the image is spread over a greater number of pixels at the edges, increasing the probability of identification.
Objects in a plane
With a rectilinear lens, objects in a common plane perpendicular to the camera have the same image resolution at the center and edge, even though the objects at the edges are farther away from the camera. This rectilinearity creates an effect called 3D stretching or lean-over, in which objects at the edges seem to be stretched (Figure 2). The wider the field of view, the more noticeable the effect.
 Click to zoom in
Click to zoom in
In Figure 3, the length of the black car seems flattened, but the widths of the twocars are the same because they are in the same plane perpendicular to the camera. This 3D stretching effect increases the resolution (pixels per foot) of objects at the edge; for lenses with barrel distortion, objects at the edge will be curved and smaller than those in the center.
 Click to zoom in
Click to zoom in
Objects in an ARC
With a rectilinear lens, the calculation of resolution of objects in an arc with the camera at the center is more complicated. As an object moves from the center of the image toward the edge in an arc without changing the distance to the camera, the object will increase in resolution significantly. Figure 4 shows the resolution increase as objects move around the arc at constant distance from the camera. The person standing 11.5 feet from the camera will increase in width due to 3D stretching as he moves to the edge; lenses with barrel distortion will not show an increase in object width.
 Click to zoom in
Click to zoom in
Resolution calculator
Given a lens and camera, it is possible to calculate image resolution. If the field of view is not known, it can be calculated for a rectilinear lens using the equation below. If the lens has barrel distortion, look up the HFOV in the specification sheet.
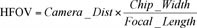
Once the HFOV is calculated and the camera known, image resolution is simply the ratio of the pixels to HFOV.
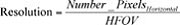
The variables in the equations depend on both lens and camera choices. Different camera resolutions have different chip sizes, resulting in different fields of view with the same lens. The table below illustrates the data for the most common megapixel cameras.
 Click to zoom in
Click to zoom in
There are many definitions of resolution, and the two most commonly used in security are total number of pixels in a camera and the pixels per foot in an image. As the total number of pixels increases, the detail in the image or the field of view or both can be increased.